二元线性回归分析
二元,有两组数据;线性,数据($a_1, a_2, a_3, …, a_n$)之间的关系,可以用公式$a_1b_1+a_2b_2+…+a_nb_n+b_0=0$进行表示;回归,建立数据之间的关系就叫做回归,对于二元数据,公式表示即为$Y=f(X)$,其中X为自变量,Y为因变量或响应变量。
问题
给出了某地区8名儿童年龄(岁)和尿肌酐(mmol/24h)。
1
2
|
年龄X = (13, 11, 9, 6, 8, 10, 12, 7)
尿肌酐含量Y = (3.54, 3.01, 3.09, 2.48, 2.56, 3.36, 3.18, 2.65)
|
问:该地区儿童的年龄和尿肌酐含量之间是否有某种关系?
数据展示
为了直观的观察数据之间的关系,我散点图进行绘制
1
2
3
4
5
6
7
|
# python imports
import numpy as np
from matplotlib import pyplot as plt
import matplotlib.gridspec as gridspec
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
import matplotlib as mpl
|
1
2
3
4
5
6
7
8
|
# Plot relation between X and Y
X = np.array([13, 11, 9, 6, 8, 10, 12, 7])
Y = np.array([3.54, 3.01, 3.09, 2.48, 2.56, 3.36, 3.18, 2.65])
plt.plot(X,Y,'x')
plt.xlabel('Age(year)', fontsize=15)
plt.ylabel('Cr(mmol/24h)', fontsize=15)
plt.title('Fig. 1. Relation between age and Cr')
plt.grid()
|
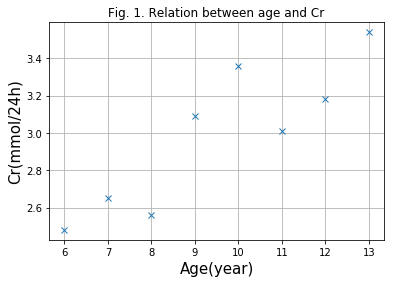
直线回归方程
从图标中可以看到,两者之间的关系可能是线性相关的。那么,我们就可以知道两者之间的关系可以表示为:
$$\hat{Y}=f(X)=aX+b\mbox{ (1)}$$
其中$X$表示表中的年龄,$\hat{Y}$表示通过线性方程估计得到的对应年龄下的尿肌酐的含量,$a$和$b$分别表示需要求的斜率与截距。$Y$表示表中实际的尿肌酐的含量。
$a$和$b$的求解可以通过多种方式实现。此处介绍了两种:1. 基于算式的,2. 基于多步逼近。
基于算式求解
求解$\hat{Y}=aX+b$对$Y$最准确的估计,就是需要使得预估值和实际值之间的距离最小,即:使得
$$\delta=\sum(\hat{Y}-Y)^2\mbox{ (2)}$$
达到最小。关于函数最小值的求解,可以联想到导数,又因为此处有两个未知变量,可以进一步联想到偏导函数$a$,$b$进行求导,得:
$$\frac{\partial\delta}{\partial a}=2\sum{(\hat{Y}-Y)\frac{\partial\hat{Y}}{\partial a}}=2\sum{(aX+b-Y)X}\mbox{ (3)}$$
$$\frac{\partial\delta}{\partial b}=2\sum(\hat{Y}-Y)\frac{\partial\hat{Y}}{\partial b}=2\sum(aX+b-Y)\mbox{ (4)}$$
从公式(2)中很容易的可以得出,$\delta$只有最小值,没有最大值。因此,当两个偏导数均为0的时候,就是$\delta$达到最小的时候。则:
$$2\sum{(aX+b-Y)X} = 2(a\sum{X^2}+b\sum{X}-\sum{XY})=0\mbox{ (5)}$$
$$2\sum{(aX+b-Y)} = 2(a\sum{X}+nb-\sum{Y})=0 \mbox{ (6)}$$
其中n为X样本的个数。对式子(5)和(6)进行求解,得:
$$a=\frac{\sum{XY}-\frac{\sum{X}\sum{Y}}{n}}{\sum{X^2}-\frac{(\sum{X})^2}{n}}\mbox{ (7)}$$
$$b=\frac{\sum{Y}}{n}-a\frac{\sum{X}}{n}\mbox{ (8)}$$
1
2
3
4
5
6
7
|
#Calculate using math
n = len(X)
a = (np.sum(X*Y) - (np.sum(X)*np.sum(Y))/n)/(np.sum(X*X)-np.sum(X)**2/n)
b = np.sum(Y)/n - a*np.sum(X)/n
YEstimation = a*X + b
delta = np.sum((Y-YEstimation)**2)
print("a = {}, b = {}, delta = {}".format(a, b, delta))
|
a = 0.13916666666666663, b = 1.661666666666667, delta = 0.23275833333333312
1
2
3
4
5
6
7
|
plt.plot(X,Y,'xk')
plt.plot(X,YEstimation, 'b')
plt.xlabel('Age(year)', fontsize=15)
plt.ylabel('Cr(mmol/24h)', fontsize=15)
plt.title('Fig. 1. Relation between age and Cr')
plt.grid()
|
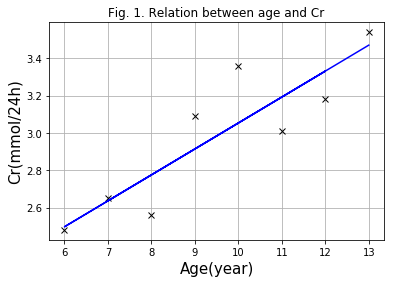
基于多步逼近
在现实过程中,有很多问题,并没有像二元线性问题这么简单,能够直接通过公式求解的方式得到最优解。而是需要对要求参数的初始值进行一定的猜测,然后通过逐步优化的方式,去逼近最优解。下面就借助二元线性问题,对这个过程进行模拟。通过公式(2)和公式(1)可以得到,当$a$(或$b$)不变的时候,$\delta$和$b$(或$a$)之间是二次多项式的关系。下面可以,通过图例给出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
# \brief Get Estimate Y value from a and b
def GetEstimateY(a, b):
return a*X + b
def GetCost(a, b):
return np.sum((Y - GetEstimateY(a,b))**2)
a0 = np.arange(-5,5,0.2)
b0 = np.arange(-5,5,0.2)
aa0, bb0 = np.meshgrid(a0, b0)
nrow,ncol = aa0.shape
cc0 = np.zeros((nrow,ncol))
for i in range(nrow):
for j in range(ncol):
cc0[i,j] = GetCost(aa0[i,j], bb0[i,j])
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(aa0, bb0, cc0)
ax.set_xlabel('a')
ax.set_ylabel('b')
ax.set_zlabel('$\delta$')
ax.set_title('Fig 2. relation between a, b and $\delta$')
|
<matplotlib.text.Text at 0x7f15c03243c8>
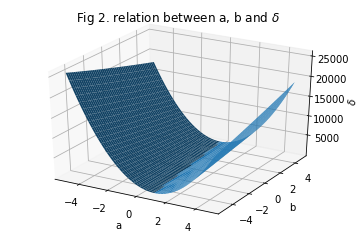
多步逼近的方法:
- (1) 首先需要对a和b的初始值进行设定,令$a=3,b=2$(此处不一定是3和2,也可以是别的值);
1
2
3
|
# Step 1. initialize a and b
def Step1():
return (2, 3)
|
- (2) 按公式(2),(3),(4)分别求得,$\delta$,$\frac{\partial{\delta}}{\partial{a}}$,$\frac{\partial{\delta}}{\partial{b}}$;
1
2
3
4
5
6
7
|
# Step 2. calculate delta, deltaA, deltaB
def Step2(a, b):
delta = GetCost(a, b)
deltaA = 2*np.sum((a*X+b-Y)*X)
deltaB = 2*np.sum((a*X+b-Y))
return (delta, deltaA, deltaB)
|
先来看下当其中一个值固定时,另一个值和$\delta$之间的关系。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
(a,b) = Step1()
(delta, deltaA, deltaB) = Step2(a,b)
print("delta = {}, deltaA = {}, deltaB = {}".format(delta, deltaA, deltaB))
# plot vb Vs vdelta
vb = np.arange(-50,50,0.2)
vdelta = np.zeros(vb.shape)
for ib in range(vb.shape[0]):
vdelta[ib] = GetCost(a, vb[ib])
plt.figure(figsize=(10,3))
gs1 = gridspec.GridSpec(1, 2)
gs1.update(wspace=1,hspace=5)
p1 = plt.subplot(gs1[0])
p2 = plt.subplot(gs1[1])
p1.plot(vb,vdelta,'k')
p1.plot(b, delta, 'bo')
p1.plot(vb, deltaB*vb+delta-deltaB*b, 'r-')
p1.set_xlabel('$b$', fontsize=15)
p1.set_ylabel('$\delta$', fontsize=15)
p1.set_title('Fig. 3. Relation between b and $\delta$ when a = 2')
p1.set_ylim([-1000,25000])
p1.grid()
# plot va Vs vdelta
va = np.arange(-5, 5, 0.1)
vdelta = np.zeros(va.shape)
for ia in range(va.shape[0]):
vdelta[ia] = GetCost(va[ia], b)
p2.plot(va,vdelta,'k')
p2.plot(a, delta, 'bo')
p2.plot(va, deltaA*va+delta-deltaA*a, 'r-')
p2.set_xlabel('$a$', fontsize=15)
p2.set_ylabel('$\delta$', fontsize=15)
p2.set_title('Fig. 4. Relation between a and $\delta$ when b = 3')
p2.set_ylim([-10000,20000])
p2.grid()
|
delta = 3038.608300000001, deltaA = 3046.78, deltaB = 304.26
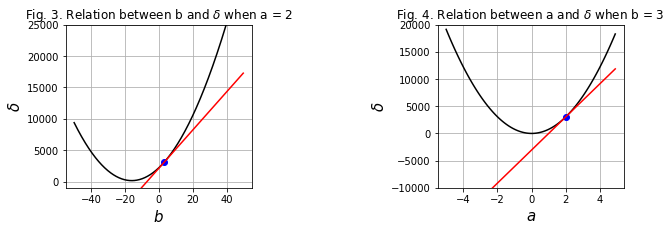
Fig3显示了当a固定的时候$\delta$和$b$之间的关系,其中蓝点是对应的$(b,\delta)$。红线为该点对应的切线。那么显而易见,为了使得$\delta$达到最小值,需要让蓝色的点往谷底移动,这就是第三个步骤;
为了避免错过最小值的情况,需要当点靠近最小值的时候,减小蓝点调整的步幅。而当蓝色的点越靠近最小值的时候,该点的切线的斜率越来越接近0,因此可以将斜率作为调整的幅度。为了对幅度的设置更加可控,在斜率的前面通常还加一个系数,被称为learning rate。得以下公式:
$$a'=a-lr\frac{\partial{\delta}}{\partial{a}}\mbox{ (9)}$$
$$b'=b-lr\frac{\partial{\delta}}{\partial{b}}\mbox{ (10)}$$
1
2
3
|
# Step 3 Adjust a and b
def Step3(a, b, deltaA, deltaB, lr):
return (a-lr*deltaA, b-lr*deltaB)
|
- (4) 重复执行第二,第三步直到$\delta$达到预期值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
(a,b) = Step1()
nLoop = 10000
lr = 0.0001
(delta, deltaA, deltaB) = Step2(a,b)
vdelta = []
vdelta.append(delta)
for i in range(nLoop):
(a, b) = Step3(a, b, deltaA, deltaB, lr)
(delta, deltaA, deltaB) = Step2(a, b)
vdelta.append(delta)
plt.plot(vdelta)
plt.xlabel('loop index')
plt.ylabel('$\delta$')
plt.title('Fig.5. $\delta$ change')
print("a = {}, b = {}, delta = {}".format(a, b, delta))
YEstimation_other = a*X + b
|
a = 0.09160117607897046, b = 2.139552469899989, delta = 0.3331959977484201

结果比对
1
2
3
4
5
6
7
8
|
plt.plot(X,Y,'xk', label='scatter')
plt.plot(X,YEstimation, 'b', label='math')
plt.plot(X,YEstimation_other, 'r', label='fitted')
plt.xlabel('Age(year)', fontsize=15)
plt.ylabel('Cr(mmol/24h)', fontsize=15)
plt.legend()
plt.title('Fig. 6. Relation between age and Cr')
plt.grid()
|
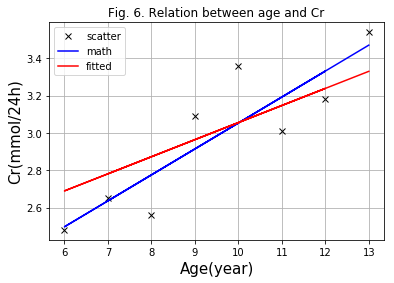
尝试
可以尝试着将循环的次数进行减少和增加,可以看到两种方式得到的结果之间差异随着循环次数nLoop的增加逐渐减少。但这个减少的趋势会越来越不明显。





