基础简介

并不像本书的其他章节，这章内容没有相关的源代码或是项目。本章，我们将讨论向量，图形渲染理论，以及OpenGL。

向量

在阅读这本书的时候，你需要熟悉代数和几何知识，但对于向量的理解并不是必要的。因为，在接下去的内容中，会对向量的基本概念作出介绍。

在面对几何或是数值相关的内容时，向量可以有很多不同的解释。在任何一种情况，向量是具有维度的。二维的向量限制在一个平面上，然而三维的向量可以在任何的物理空间。向量还可以有更高的维度，但是通常情况下，我们处理的向量的维度只在二维到四维之间。

严格的来说，向量还可以存在仅仅一维的情况。这样的向量被称为标量。

在几何术语中，向量可以表示两个概念：一个空间中的位置或是一个方向。

向量的位置表示空间中一个特殊的位置。如，在下图中我们有一个向量位置A。

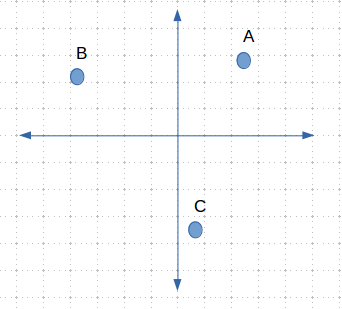figure 1 vector position Figure1 vector position

向量也可以表示为方向。方向向量没有一个原点；只用来表示空间中的方向。下图中给出了不同的方向向量，其中B和D虽然画在不同的位置，但它们是相同的方向向量。

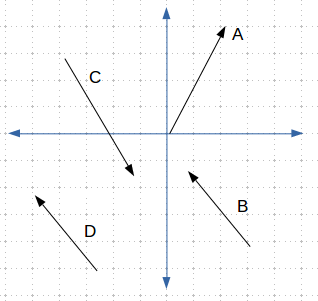figure 2 direction vectors Figure2 Direction Vectors

对于几何而言，以上的表达方式已经够用了，但是向量还可以被解释成数值。这时候，一个向量表示为一个数字序列，没一个数字表示一个维度。因此，二维的向量有两个数字；三维的向量有三个数字。对于四维向量也是一样的。从数字上来说，标量仅仅是一个数字。

向量中的没一个数字都被称为要素（component）。每一个要素都有自己的名字。对于我们而言，向量的第一个要素被成为X，第二个被成为Y，第三个是Z，第四个是W。

当用文本的方式来书写向量的时候，它们通常被括号包围。因此，一个3D向量可以是(0,2,4)，其中X为0,Y为2,Z为4.当他们以公式的形式进行书写的时候，表现形式为：

$$ \vec {a} = \left[ \begin{matrix} 1 \
2 \
3 \end{matrix} \right] $$

在数学公式中，向量变量会以粗体或是上面带箭头的形式出现。

当在绘制向量的时候，需要区分位置向量和方向向量。但是，它们两者的数值并没有区别。唯一的区别是你怎么使用它们，而不是怎么用数字表达它们。因此，你可以把一个点考虑成一个向量，然后执行一些操作，最后再将它考虑成一个点。

虽然向量的各个成分之间是独立的，但是数学公式操作它们的时候，它们是一个整体。在接下来的内容中，我们会通过几何和数值的方式展示一些操作。

向量加法 你可以对两个向量执行加法操作。从图形上看是这样的：

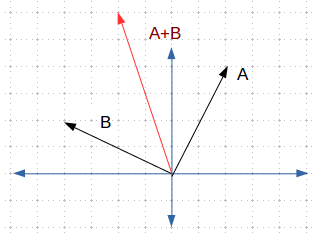figure3 vector addition Figure3 Vector Addition

要记得的是，方向向量在不改变具体数值的情况下，可以对其进行移动。因此，如果你将两个向量放置为首位相接，向量的加法可以简单的表示成从第一个向量的尾部指向第二个向量的头。

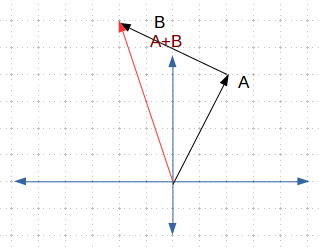figure4 vector addition head-to-tail Figure4 Vector Addition Head-to-Tail

从数值上来讲，两个向量的求和就是将两个向量的各个成分相加，

公式1. 向量相加 $$ \vec{a} + \vec{b} = \left[ \begin{matrix} a_x \ a_y \ a_z \end{matrix} \right] + \left[ \begin{matrix} b_x \ b_y \ b_z \end{matrix} \right] = \left[ \begin{matrix} a_x+b_x \ a_y+b_y \ a_z+b_z \end{matrix} \right] $$

一个操作需要对向量各个成分进行，被称为分量操作（component-wise operation）。向量加法就是一个分量操作。任何一个分量操作都需要保证两个向量有相同的维度。

向量求反和减法 你可以对一个向量去反，就是逆转一个向量的方向。

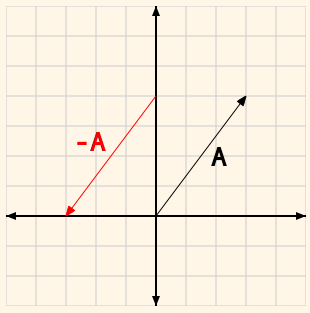figure5 vector negation Figure5 Vector Negation

从数值上来看，就是对向量中的每个成分都去反。

公式2. 向量去反

$$-\vec{a}=-\left[\begin{matrix}a_x \ a_y \ a_z \end{matrix} \right]=\left[\begin{matrix} -a_x \ -a_y \ -a_z \end{matrix} \right]$$

正如数值运算，向量的减法就是一个向量和第二个向量的反进行相加。

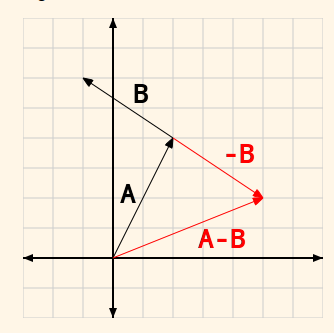Figure6 Vector Subtraction

向量乘法 向量乘法操作是向量操作中为数不多的没有几何概念与之对应的操作。将两个方向或是两个位置进行相乘，并没有什么意义。但这并不是说向量的乘法没有作用。

数值上，向量的乘法，就是将对应的各个成分相乘。

公式3. 向量乘法

$$ \vec{a}\vec{b}=\left[\begin{matrix} a_x \ a_y \ a_z \end{matrix}\right]\left[\begin{matrix}b_x \ b_y \ b_z \end{matrix}\right]=\left[\begin{matrix} a_xb_x \ a_yb_y \ a_z*b_z \end{matrix}\right]$$

向量缩放操作 向量可以乘以一个标量。这个标量仅仅是一个数值。更具这个标量的值，这个向量可能被放大或缩小。

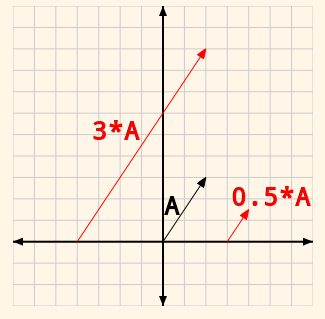Figure7 Vector Scaling

数值运算上，就是将向量的各个成分和标量进行相乘。

公式4. 向量缩放操作

$$ s*\vec{a}=a*\left[\begin{matrix} a_x \ a_y \ a_z\end{matrix}\right]=\left[\begin{matrix} s*a_x \ s*a_y \ s*a_z \end{matrix}\right] $$

标量也可以和向量相加，这同样没有什么几何意义。公式如下：

公式5. 向量标量相加

$$s+\vec{a}=s+\left[\begin{matrix} a_x \ a_y \ a_z\end{matrix}\right]=\left[\begin{matrix}s+a_x \ s+a_y \ s+a_z \end{matrix}\right]$$

向量代数 理解这些向量操作之间的关系是有帮助的。

向量加法乘法遵循很多和标量加法乘法相同的规则。它们是交换率，结合率，和分配率。

公式6. 向量代数

  • 交换率：$\vec{a}+\vec{b}=\vec{b}+\vec{a}$, $\vec{a}\vec{b}=\vec{b}\vec{a}$
  • 结合率：$\vec{a}+\left(\vec{b}+\vec{c}\right)=\left(\vec{a}+\vec{b}\right)+\vec{c}$, $\vec{a}\left(\vec{b}\vec{c}\right)=\left(\vec{a}\vec{b}\right)\vec{c}$
  • 分配率：$\vec{a}\left(\vec{b}+\vec{c}\right)=\left(\vec{a}\vec{b}\right)+\left(\vec{a}*\vec{c}\right)$

向量和标量具有类似的特性。

长度. 向量也有长度，表示从起点到终点的距离。

公式7. 向量长度

$$ |\vec{a}|=\sqrt{a_x^2+a_y^2+a_z^2}$$

这里使用了毕达哥拉斯定理来计算向量的长度。这个适用于任何维度的向量，并不单单是二维或三维向量。

单位向量与标准化 一个向量的长度为一，那么这个向量是 单位向量 。在数学公式中单位向量的表示方式是在变量名上面加个^。

一个向量转变成单位向量的过程叫做 标准化 。将向量除以改向量的长度就能够得到它的长度。

公式8. 向量标准化

$$\hat a =\frac{1}{|\vec{a}|}*\vec{a}=\left[\begin{matrix} \frac{a_x}{|\vec{a}|} \ \frac{a_x}{|\vec{a}|} \ \frac{a_x}{|\vec{a}|} \end{matrix}\right]$$

这些并不是本书中用到的所有的向量操作。新的向量操作会在它们第一次被使用到的时候进行介绍。并且，并不像这里使用到了公式，它们中的大多数将不是针对各个成分的独立操作。

范围符号 本书中会使用标准的标识来标记一个值的具体范围。

如果一个值在0～1之间，并且可以等于0和1,那么标记为[0, 1]。放括号表示范围包括了相邻的值。

如果一个值在0～1范围，但不包括0,那么标记为(0, 1]。圆括号表示相邻的值并不包括在范围内。

如果一个值表示0和大于0的任何数值，那么标记为$[0, \infty)$，需要注意的是无穷大是不可达到的，因此它总是被排除在范围之外的。任何一个小于0的范围则标记为$(-\infty,0)$。

图形和渲染

接下去的内容对渲染的过程进行粗略介绍。遇到的部分内容不是很明白也没有关系，在接下去的章节中，会被具体阐述。

你在电脑屏幕上看到的任何东西，包括你现在阅读的文字是简单的二维像素点的集合。如果你在屏幕上截图，并放很大，就会看到一个个的方格。

Figure8. An Image

没一个格子就是一个像素。pixel单词，是从Picture Element中提取出来的。你屏幕上的没一个像素都有一个独立的颜色。二维的像素数组就组成了 图像

因此，任何一种图像操作的目的都是确定将什么颜色放到哪个像素上。不同颜色在不同像素位置的设定形成了文字，窗口，等其他东西。

既然所有的图像都是二维的像素组成的，那么3D图像是怎么来的呢？3D图像是一系列带颜色的像素组成的，并且给人的视觉上看上去像是一个3D的世界，而不是单纯的2D的图。这个将3D的世界转变成2D图像的过程叫做 渲染 。

3D图像的渲染有不同的方法。实时图形显卡中引入了一种很巧妙的方法来实现渲染。这个过程被称为光栅化，实现光栅化的系统被成为 光栅器(rasterizer) 。

通过光栅，你看到的所有的对象都是空壳。有一些技术可以用来将这些空壳打开，但是这样也仅仅是用一部分壳替换了另一部分的壳。其实所有的东西都是壳（shell）。

上面这段话，可以理解成，所有的对象都是由不同的等直面组成的，就好比在一个鸡蛋壳里面，有鸡蛋壳，一层套这一层，当将最外面的壳打开后，你能够看到里面的壳（等值面）。

这些壳都是由三角形组成的。即使是那些看起来非常平滑的曲面，如果很靠近的去观察它，可以发现它其实也是由壳组成的。有技术可以产生更多的三角形，使得物体之间看起来更加接近或是更加大，以至于观察者几乎看不到物体的侧面。不过，它们也都是由三角形组成的。

上面这段话意思是，鸡蛋壳，通过光栅器，看到的并是不光滑的面，而是由一个个小三角形组成的，并且靠近观察者的地方，小三角形看起来比较大，而在远离观察者的地方，如靠近侧面，小三角形看起来就比较密。另一面的内容，你无法看到，但是它还是由许多小三角形组成的。

注意事项 一些光栅的实现使用的是平面四边形：拥有四条边，并且所有的点都在一个平面上。硬件使用的光栅在原理上使用三角形的原因是，三角形能够保证所有的边都能够在一个平面上。这样可以很大程度的简化光栅化的过程。

一个对象的外表面是由一系列相邻的三角形组成的。这样的一系列的三角形通常被称为 geometry , model 或者是 mesh 。这些术语会被交换的使用。

光栅化的过程拥有几个阶段。这些阶段按顺序归入到一个pipeline中，最开始的是输入的一系列三角形，最终输出的是2D图。这也是回升么光栅化的过程是易于硬件加速的：按照特定的顺序，每一次都对一个三角形进行操作。三角形可以在pipeline的开始阶段输入，然而更早输入的三角形也可以出现在光栅化的某个阶段。

三角形和各种网格的输入顺序会影响它的输出结果。需要记住的是，不管你怎样输入三角形网格数据，光栅都将以一定的顺序处理各个三角形，当前一个三角形被处理完了之后，才会处理下一个三角形。

OpenGL有获取基于硬件的光栅的API。正因为这样，它会使得模型适用于光栅化的渲染。光栅会接受用户输入的一些列三角形，然后针对这些三角形进行操作，并将像素结果输出。这个过程简单描述了OpenGL中光栅的工作机制，但，对于我们而言是足够了。

三角形和顶点. 三角形包括三个顶点。 顶点可以是任何数值。为了简单起见，我们约定顶点是三维空间上有值的点。任何三个不再一条直线上的点可以组成一个三角形。因此，我们可以得到的信息是，一个三角形包含3个有三个维度的点。

三维空间中的一个点，含有三个分量，分别是x，y，z轴。通常用一下形式表示$(X,Y,Z)$。

光栅化概述

光栅化的流程对于现代硬件来说是非常复杂的。这里非常简单的概述了整个流程。在我们进一步通过OpenGL学习渲染之前，有必要对这个流程有一个初步的认识。更详细的人荣处理更高层次的概述，是没有办法讲清楚的。

裁剪空间转换 光栅化的第一步是将三角形中的每一个顶点转化到特定的空间区域。在空间体中的任何东西都会被渲染到输出图像中，在空间体外的其他内容是不会渲染到图像中的。这个区域与用户想要渲染的位置有关。

这个三角形即将被转换到的空间，在OpenGL中的称呼为， 裁剪空间 clip space 。三角形的定点在裁剪空间中的位置被称为 裁剪坐标 。

裁剪坐标和常规的点有一点区别。一个点在3D空间中有三个坐标轴。一个点在裁剪空间有4个坐标轴。前三个是X，Y，Z，第四个被称为W。最后一个坐标实际上定义了这个定点的裁剪空间的范围。

在裁剪空间，X的正方向是向右，Y的正方向是上，Z的正方向是原理观察者。

顶点位置转换到裁剪空间的过程有很多途径。OpenGL提供了很多灵活的方式。对于这个过程在以后的章节中会详细的介绍。

因为裁剪空间是世界中的可见部分转换而来的，所以任何在这个区域外的三角形会被抛弃掉。任何部分在裁剪空间外的三角形，都有经历 裁剪 的过程。这个过程将一个三角形分割成一些小的三角形，使得所有的三角形都能够在裁剪空间中。因此，这个空间就被称为“裁剪空间”。

标准化坐标 裁剪空间比较有意思，但是并不是很方便。这个空间的大小对每一个顶点来说是不一样的，这使得一个三角形的可视化变得非常困难。因此，裁剪空间会被转换成更加合理的坐标空间： 标准化设备空间 。

这个过程非常发简单，就是将每一个顶点的X，Y，Z除以W，就能够得到标准化设备空间。

标准化设备空间，除了它的X，Y，Z坐标范围为[-1,1]以外，其实就可以理解成裁剪空间。两个空间坐标系的方向是一致的。除数W，在将3D的三角形投影到2D的图像的时候，起到了非常重要的作用；我们将在后续的内容中进一步说明。

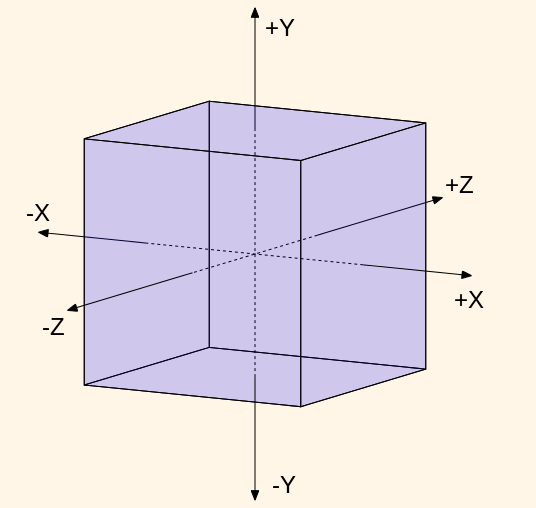Figure9. Normalized Device Coordinate Space

这个立方体，表示标准设备空间的边界。

窗口转换 接下去的一个阶段是再次变换每个三角形的顶点。这一次是将标准设备坐标系转换到 窗口坐标系 。从名字上可以看出，窗口坐标系就是OpenGL运行的窗口。

尽管它指的是窗口，但仍然是三维的坐标系。和裁剪空间一样，X是右方向，Y是上方向，Z是远离观察者的方向。唯一不同的是，这些轴的范围依赖于看到的窗口。还有一点需要注意的是，虽然这些点都在窗口坐标系中，但是点的精度并没有损失。点并没有成为整数点，依然是浮点数，因此点的精度和单个像素是不一样的。

Z的范围是[0,1]，0表示最近的，1表示最远的。在这个范围以外的点是不可见的。

需要注意的是，窗口坐标系中，左下角的位置是原点(0,0)。这个与用户通常认知中的屏幕坐标系，左上角是原点是不一样的。如果你想要，通过一定的更改，可以将变换变换到左上角是原点的坐标系中。

这个过程会在辅助材料中进行详细讨论。

扫描转换 Scan Conversion 将三角形的顶点转换到窗口坐标系后，这个三角形还得经历 扫描转换 的过程。这个过程就是依据三角形覆盖的像素点的位置，将三角形分解成不同的像素的过程。

Figure10. Scan Converted Triangle

中间的图显示了输出图像的像素格子的大小；圆圈表示了每个像素的中心位置。每一个像素的中心表示一个 取样(sample) ：像素区域内的离散位置。在扫描转换中，一个三角形将会在三角形3D区域内部每一个像素取样的位置产生一个 碎片(fragment) 。

右边的图像显示的就是通过扫描转换产生的碎片。这个产生了三角形形状的一个近似。

待渲染的三角形有公共的边是一个很常见的事情。只要公共的定点是相同的，OpenGL就能够保证扫描转换出来的结果中，两个三角形之间没有采样间隔。

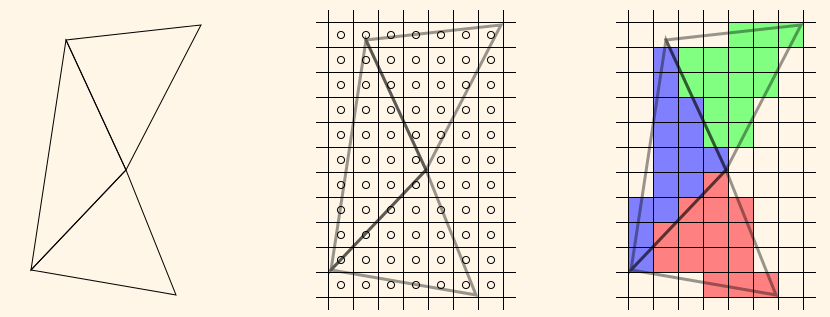Figure11. Shared Edge Scan Conversion

为了更简单的使用扫描转换，OpenGL同时也保证相同的输入，能够得到完全相同的渲染输出。这个也被称为， 不变性保证 。因此，需要用户保证使用相同的输入点，来获得没有间隔的扫描转换。

扫描转换是一个固有的2D操作。这个过程仅仅使用了三角形在窗口坐标系中的X和Y的值，来确定需要产生哪些碎片。不要忘了Z值，但是Z值和三角形扫描转换并没有直接的关系。

三角形扫描变化的结果是覆盖在三角形上的有顺序的碎片。每一个碎片都有一个数值与它关联。这个数值包括了碎片在窗口坐标系中的2D位置，同时也有Z的位置。Z值是碎片的深度。还有一些与碎片相关的其他参数，这将在后续的内容中阐述。

碎片处理（Fragment Processing）

这个阶段，通过扫描转换将得到的碎片设置一种或更多的颜色，和一个深度值。单个三角形中的碎片被处理的顺序是无关紧要的，因为一个三角形位于同一个平面上，产生的碎片不会有重叠的可能。但是，可能和另一个三角形的碎片发生重叠。由于光栅器中顺序的重要性，使得一个三角形中的碎片必须在另一个三角形的碎片处理之前处理完。

这个阶段有很大的自由性，OpenGL的用户有各种不同的选择来决定要赋予碎片的颜色。在辅助教材中，我们会展开详细的论述。

碎片输出（fragment writing） 在产生一个或多个颜色值和一个深度信息之后，这个碎片会输出到目标图像中。这个过程不单单是将颜色信息赋值到图像上。需要经过计算，才能将碎片的将颜色和深度信息以及图像中已经有的颜色信息一起融合到一块。在不同的章节中都会涉及到这部分的内容。

颜色

正如前面所述，一个像素表示图中拥有特定颜色的一个元素。一个颜色可以以很多不同的方式展现。

在计算机图形学中，对颜色的描述通常是不同通道下[0,1]范围内的数字组成。最终的颜色是各个通道下颜色的组合。

各个通道下颜色的集合叫做 颜色空间 。最常见的颜色空间就是RGB颜色空间，该颜色空间有三个颜色通道，分别是红，绿，蓝。针对打印的颜色空间通常是CMYK（Cyan青色，Magenta洋红，Yellow黄色，Black黑色）。由于我们处理的场景是将图像渲染到屏幕上，因此我们使用的颜色空间是RGB颜色空间。

注意 你也可以对可编程的着色器进行一些特殊的处理，来允许你对不同的颜色空间进行操作。因此，从技术上来说，我们仅仅需要将结果输出到线性的RGB颜色空间即可。

因此，在OpenGL中一个像素有三个[0,1]范围的值，用来表示RGB颜色空间中的RGB三个分量。将这三个颜色的不同大小进行组合，我们能够得到成千上万的不同的颜色。当我们处理透明度的时候，这个还会得到进一步的扩展。

着色器

着色器 被设计用来在渲染器上运行部分操渲染操作的程序。不管使用的渲染系统的类型，着色器只能在渲染过程中特定的过程被使用。这些 着色阶段（shader stages） 指的是用户可以添加任意算法实现特别视觉效果的位置。

根据上面总结出来的光栅化过程，有几个着色阶段的实现既保证了运行的性能，有向用户提供了可编程的简易性。例如，将定点转换到裁剪坐标系，有比如将碎片设定特定的颜色和深度。

OpenGL的着色器是运行在渲染硬件上的。这样可将CPU空置出来执行其他的任务，或者如果没有执行任意代码的灵活性，那么简单的执行一些操作也将是困难的事情。这样的缺点是，着色器的使用是有一定限制的，而CPU是没有限制的。

目前有各种各样的着色器语言。本书中使用的是OpenGL的主要的着色器语言，被称为“OpenGL Shading Language”，简称GLSL。它的语法看着非常像C语言，但并不是C语言。

OpenGL是什么

在我们编写openGL程序之前，我们首先需要知道什么是OpenGL。

将OpenGL作为一个API

OpenGL 通常被认为是应用程序接口（API）。OpenGL API有不同编程语言的实现版本。但是，它们最终使用的都是最底层的C语言的接口。

在C语言的API中，定义了很多typedefs，#define，以及函数。typedefs用于定义openGL里面使用到的基本的数据类型，如GLint，GLfloat等。

复杂的数据结构，如struct，在openGL中没有直接暴露给用户，都是隐藏在一系列的API背后。这样有利于将OpenGL API改写成非C语言实现的版本。

在C++中，如果你想要一个包含整型，浮点型和字符串的类型，你会采取下面的措施实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

struct Object
{
    int count;
    float opacity;
    char *name;
}

// Create the storage for the object
Object newObject;

// Put data into the object
newObject.count = 5;
newObject.opacity = 0.4f;
newObject.name = "Some String";

在opengl中，采用api的方式实现，如下：

1
2
3
4
5
6
7
8
9

// Create the storage for the object
GLuint objectName;
glGenObject(1, &objectName);

// Put data in to the object
glBindObject(GL_MODIFY, objectName);
glObjectParameteri(GL_MODIFY, GL_OBJECT_COUNT, 5);
glObjectParameteri(GL_MODIFY, GL_OBJECT_OPACITY, 0.4f);
glObjectParameteri(GL_MODIFY, GL_OBJECT_NAME, "Some String");

上述的例子中，并不是真实的opengl的命令，仅仅用来说明，在opengl中一个对象是怎么通过api的方式创建以及赋值的。

opengl自己拥有存储所有opengl对象的存储空间。因此，用户只能够通过引用的方式来访问对象。几乎所有的opengl对象都会被绑定到一个非符号整型（GLuint）。对像会被类似于glGen*的函数创建，星号表示的对象的类型。第一个参数表示有多少个对象要被创建，第二个参数用来接受创建的对象的名字。

大多数对象首先需要被绑定到上下文，才能够被更改。很多对象可以被绑定到上下文的不同的位置，这就允许一个对象以不同的方式被使用。这些不同的位置被称为“targets”，所有的对象都拥有一个合法的目标列表，有些对象仅有一个目标。在上面的例子中，GL_MODIFY是objectName被绑定到的位置。

GL_OBJECT_*形式命名的枚举，是这个对象中能够被赋值的属性。glObjectParameter这类的函数，作用是将对象中的参数绑定到给定的目标上。由于opengl的api是c语言版本的，对于不同类型入参的函数，必须以不同函数名分别开来，如glObjectParameteri针对整型入参，glObjectParameterf针对浮点型入参。

需要注意的是，opengl中的对象并不是都想示例中这么简单，有些改变对想法状态的函数，也和示例中函数的形式不同。那么，将一个对象绑定到上下文具体是什么意思呢，在下面会有解答。

opengl的结构

opengl的api被定义为状态机。几乎所有的opengl函数都是设置或是获取相应的状态。没有用来改变对象状态的唯一一类函数是，利用这些设进去的状态，来触发渲染的行为。

你可以将这个状态机设想成一个很大的，带有很多不同属性的数据结构。这样的数据结构被称为“opengl context”，上下文中的每一个属性都包含了一些用于渲染的必要的信息。

opengl中的对象被定义成上下文中的一系列的属性，并且可以被保存和恢复。将一个对象绑定到一个目标，就是将对象中的属性替换掉上下文对应目标上的属性。因此在绑定之后，后续的函数将会从上下文中调用到刚刚更新了的内容。

对象通常用GLuint表示，这些整数是链接opengl实际对象的句柄。0是一个特殊的数字，与null指针具有类似的含义。将目标绑定到0,意味着对当前绑定的对象解绑。也就是说，对应的上下文中的内容会恢复到初始状态，恢复到绑定发生之前的状态。

opengl上下文类似于：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

// Opengl Object Example
struct Values
{
    int iValue1;
    int iValue2;
};

// Opengl Context Example
struct OpenGL_Context
{
    ...
    Values *pMainValues;
    Values *pOtherValues;
    ...
};

OpenGL_Context context;

要创建一个Values对象，你将要调用类似与glGenValues的函数，然后你要将创建的对象绑定到上下文的目标位置，如GL_MAIN_VALUES表示指针context.pMainValues，GL_OTHER_VALUES表示指针context.pOtherValues。你将通过glBindValues分别将对象绑定到对应的目标上。这将会使得上下文中的指针指向你创建的对象。

也有用于设置绑定对象内参数的函数，glValueParam。它将获取对象的目标位置，也就是上下文中的那个指针。也会获取一个枚举用来表示对象中的哪个值会被改变。如GL_VALUE_ONE来表示iValue1，GL_VALUE_TWO用来表示iValue2。

opengl规范

从技术上来说，opengl并不是api，而是一个规范。一个文档。c api仅仅是对这个规范的一种实现。这个规范定义了opengl初始状态，每一个函数对于改变状态和获取状态能够做些什么，当你调用渲染函数的时候，哪些会发生。

这个规范是OpenGL架构审查委员会书写的。这个机构的代表有Apple，NVIDIA和AMD等。这个委员会是Khronos Group的一部分。

这个规范是非常复杂的技术文档。但是，其中的部分内容是很容易理解的。如果你尝试去读这个文档，你会发现这个文档注重对结果的描述，而不是具体实现。也就是说，如果硬件的一部分以不同的实现方式提供了相同的结果，用户是无法分别出来的。

opengl的实现 尽管opengl ARB控制了opengl的规范，但是它并没有控制代码本身。opengl并不能通过软件中心进行下载。它的实现完全取决于硬件开发商，根据opengl规范，进行实现。

针对不同的操作系统，都有不同的人员来控制opengl的实现。针对windows操作系统，opengl的实现是受硬件开发商自己控制的。在Mac OSX操作系统，opengl的实现是受apple公司控制的，他们决定提供给用户opengl的哪个版本，以及哪些扩展。而，针对linux系统，事情就变得有点复杂了。

简单的讲，如果你写的程序超出了规范中约定的行为，这个就是你的opengl实现商的问题了（假设你的代码中并没有bug）。在windows系统，他们的opengl实现是附带在不同的图形硬件驱动中的。因此，假如遇到了他们实现版本的问题，通常可以采用升级驱动的方法，也许这个问题已经在最新的驱动中解决了。

opengl版本 目前已经有了很多不同版本的opengl规范。opengl的版本并不像大多数通常会改变大多数api的direct3d版本。在一个opengl版本中能够运行的代码，基本可以在更新的版本中运行。

唯一需要注意的是，正确处理opengl3.0和以上的版本，和3.0之前的版本之间的关系。在3.0版本的时候，让很多旧接口过时了。在3.1版本的时候将这些过时的接口中的大部分都删除了。同时将规范分解成了两个变种，核心的和兼容的。兼容的部分包含了3.1版本删除的所有旧的函数，然而在核心的部分并没有这么做。理论上，opengl规范仅仅需要核心的部分，但是这会让很多原来以来于老接口函数的功能无法正常工作。

作为一个实际问题，这些都不重要。没有一个opengl驱动开发者会仅仅实现核心的部分。因此，opengl完全是向下兼容的。

术语

  • vector 向量

一个由带顺序的其他数值组成的值。向量中存储的数字的个数称为维度。向量拥有属于自己的数学操作。

  • scalar 标量

单个，非向量数值，也可以考虑成是一个维度的向量。

  • vector position 位置向量

表示一个位置的向量

  • vector direction 方向想量

表示一个方向的向量

  • vector component 向量组成成分

向量中的每一个值

  • component-wise operation 面向向量各成分的操作

一个操作的效果是分别对向量各个成分进行操作的效果相同，输出结果的向量的维度和输入向量的维度相同。

  • unit vector 单位向量

向量长度为1的向量是单位向量，是纯粹的方向向量

  • vector normalization 向量标准化

将一个向量变成同向的单位向量的过程

  • pixel 像素

数字图像的最小成分。一个像素拥有颜色空间中的特定颜色

  • image 图像

二维的像素数组

  • rendering 渲染

将一个3d的世界，从一个特殊的视角转变成2d图像的过程

  • rasterization 光栅话

一个特殊的渲染方法，用于将一系列的3d的三角形转变成2d的图

  • geometry，model，mesh

由三角形组成的，3d空间中的单个物体

  • vertex 顶点

组成三角形的三个元素之一。顶点可以是任意的数字，用来表示一个点在3d空间中的位置。

  • clip space, clip coordinates 裁剪空间，裁剪坐标系

由三维空间中的点转换而来，这个空间中点的位置是4个维度的。第四个维度w表示了裁剪空间的可见区域。因此裁剪坐标系中点的xyz成分必须在[-w,w]之间才是可见的。在裁剪坐标系中x的正方向是右，y的正方向是上，z的正方向是远离观察者的方向。裁剪坐标系中的点是渲染管线中的顶点处理阶段的输出结果。

  • clipping 裁剪

这个过程是将裁剪坐标系中如果有顶点在裁剪空间外面，就发生分割行为

  • normalized device coordinates 标准化设备坐标系

这个是将裁剪坐标系中的点除以w之后的点。这样，所有的点的成分在[-1,1]范围内就是可见的。

  • window space， window coordinates 窗口空间，窗口坐标系

由标准化设备坐标系映射过去的三维空间。这些点的xy的位置和最终图像的位置是一一对应的。原点在左下方，x正方向为右，y正方向是上。z值在[0,1]的范围，0表示最近，1表示最远。在这个范围外的点是不可见的。

  • scan conversion 扫描转换

这个过程是将窗口坐标系中的三角形，打成一个个片段，然后投射到对应的图像的像素中。

  • sample 采样

在扫描转换过程那个中对于三角形像素边界非连续的位置判断是否产生片段的过程。单个像素的区域可以进行多次采样，从而可以产生过的片段

  • fragment 片段

扫描转换后的三角形的单个元素。一个片段可以包含任何的数值，但是这个数值要是三维的，用来表示窗口坐标系中在三角形中的位置。

  • invariance guarantee 不变性保证

opengl提供的一个保证，在顶点处理过程中相同的输入拥有相同的输出。

  • colorspace 颜色空间

在计算机图形学中，用来表示颜色的一个集合。所有的颜色都是在特定的颜色空间的基础上定义的。

  • shader 着色程序

渲染器来执行的程序，用来执行用户定义的一些行为

  • shader stage 着色器

渲染管线中的一个特殊位置，着色程序用来执行的地方。这个阶段的执行结果将会作为下一个阶段的输入。

  • opengl

用来规定渲染系统的规范

  • opengl context opengl上下文

会用于渲染的参数的特殊集合。类似于一个很大的c语言中的struct，其中包含了很多不同的可以被访问的属性。如果你需要创建多个窗口来处理渲染任务，那么没一个窗口都会有自己独立的opengl上下文

  • object binding 对象绑定

对象可以绑定到opengl上下文的特定位置上。此时，上下文特定位置的参数指向的内容就是被绑定的对象中设定的内容。同时一个对象可以被绑定到不同的位置，特定类型的对象可以绑定到不同的位点。

  • opengl implementation opengl的实现

针对特殊的系统，对opengl规范实现的软件